|
Functions |
|
void | Tensors::Dot (Tensor2 const &A, Tensor1 const &u, Tensor1 &v) |
|
REAL | Tensors::Dot (Tensor2 const &x, Tensor2 const &y) |
| | 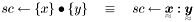
|
|
void | Tensors::Dot (Tensor2 const &x, Tensor4 const &A, Tensor2 &y) |
| | ![$ \{y\}\gets\{x\}\bullet[A] \quad\equiv\quad \TeSe{y}\gets\TeSe{x}:\TeFo{A} $](form_32.png)
|
|
void | Tensors::Dot (Tensor4 const &A, Tensor2 const &x, Tensor2 &y) |
| | ![$ \{y\}\gets[A]\bullet\{x\} \quad\equiv\quad \TeSe{y}\gets\TeFo{A}:\TeSe{x} $](form_33.png)
|
|
void | Tensors::Dot (Tensor4 const &A, Tensor4 const &B, Tensor4 &C) |
| | ![$ [C]\gets[A]\bullet[B] \quad\equiv\quad \TeFo{C}\gets\TeFo{A}:\TeFo{B} $](form_34.png)
|
|
void | Tensors::Dyad (Tensor2 const &x, Tensor2 const &y, Tensor4 &A) |
| | ![$ [A]=\{x\}\otimes\{y\} \quad\equiv\quad \TeFo{A}\gets\TeSe{x}\otimes\TeSe{y} $](form_35.png)
|
|
void | Tensors::AddScaled (REAL const &a, Tensor4 const &X, REAL const &b, Tensor4 const &Y, Tensor4 &Z) |
| | Add scaled tensors: ![$ [Z] \gets a[X]+b[Y] \quad\equiv\quad \TeFo{Z}\gets a\TeFo{X}+b\TeFo{Y} $](form_73.png) . .
|
|
void | Tensors::Ger (REAL const &a, Tensor2 const &x, Tensor2 const &y, Tensor4 &A) |
| | ![$ [A]=\alpha\{x\}\otimes\{y\}+[A] \quad\equiv\quad \TeFo{A}\gets\alpha\TeSe{x}\otimes\TeSe{y}+\TeFo{A} $](form_36.png)
|
|
void | Tensors::GerX (REAL const &a, Tensor4 const &A, Tensor2 const &x, Tensor2 const &y, Tensor4 const &B, Tensor4 const &C, Tensor4 &D) |
| | ![$ [D]=\alpha([A]\bullet\{x\})\otimes(\{y\}\bullet[B])+[C] \quad\equiv\quad \TeFo{D}\gets\alpha(\TeFo{A}:\TeSe{x})\otimes(\TeSe{y}:\TeFo{B})+\TeFo{C} $](form_74.png)
|
|
void | Tensors::Scale (REAL const &a, Tensor4 &B) |
| | ![$ [B]=\alpha([B]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{B} $](form_75.png)
|
|
void | Tensors::CopyScale (REAL const &a, Tensor4 const &A, Tensor4 &B) |
| | ![$ [B]=\alpha([A]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{A} $](form_76.png)
|
|
REAL | Tensors::Reduce (Tensor2 const &x, Tensor4 const &A, Tensor2 const &y) |
| | ![$ s=\{x\}^T[A]\{y\} \quad\equiv\quad s=\Dc{\Dc{\TeSe{x}}{\TeFo{A}}}{\TeSe{y}} $](form_77.png)
|
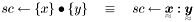
![$ \{y\}\gets\{x\}\bullet[A] \quad\equiv\quad \TeSe{y}\gets\TeSe{x}:\TeFo{A} $](form_32.png)
![$ \{y\}\gets[A]\bullet\{x\} \quad\equiv\quad \TeSe{y}\gets\TeFo{A}:\TeSe{x} $](form_33.png)
![$ [C]\gets[A]\bullet[B] \quad\equiv\quad \TeFo{C}\gets\TeFo{A}:\TeFo{B} $](form_34.png)
![$ [A]=\{x\}\otimes\{y\} \quad\equiv\quad \TeFo{A}\gets\TeSe{x}\otimes\TeSe{y} $](form_35.png)
![$ [Z] \gets a[X]+b[Y] \quad\equiv\quad \TeFo{Z}\gets a\TeFo{X}+b\TeFo{Y} $](form_73.png) .
. ![$ [A]=\alpha\{x\}\otimes\{y\}+[A] \quad\equiv\quad \TeFo{A}\gets\alpha\TeSe{x}\otimes\TeSe{y}+\TeFo{A} $](form_36.png)
![$ [D]=\alpha([A]\bullet\{x\})\otimes(\{y\}\bullet[B])+[C] \quad\equiv\quad \TeFo{D}\gets\alpha(\TeFo{A}:\TeSe{x})\otimes(\TeSe{y}:\TeFo{B})+\TeFo{C} $](form_74.png)
![$ [B]=\alpha([B]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{B} $](form_75.png)
![$ [B]=\alpha([A]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{A} $](form_76.png)
![$ s=\{x\}^T[A]\{y\} \quad\equiv\quad s=\Dc{\Dc{\TeSe{x}}{\TeFo{A}}}{\TeSe{y}} $](form_77.png)
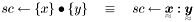
![$ \{y\}\gets\{x\}\bullet[A] \quad\equiv\quad \TeSe{y}\gets\TeSe{x}:\TeFo{A} $](form_32.png)
![$ \{y\}\gets[A]\bullet\{x\} \quad\equiv\quad \TeSe{y}\gets\TeFo{A}:\TeSe{x} $](form_33.png)
![$ [C]\gets[A]\bullet[B] \quad\equiv\quad \TeFo{C}\gets\TeFo{A}:\TeFo{B} $](form_34.png)
![$ [A]=\{x\}\otimes\{y\} \quad\equiv\quad \TeFo{A}\gets\TeSe{x}\otimes\TeSe{y} $](form_35.png)
![$ [Z] \gets a[X]+b[Y] \quad\equiv\quad \TeFo{Z}\gets a\TeFo{X}+b\TeFo{Y} $](form_73.png) .
. ![$ [A]=\alpha\{x\}\otimes\{y\}+[A] \quad\equiv\quad \TeFo{A}\gets\alpha\TeSe{x}\otimes\TeSe{y}+\TeFo{A} $](form_36.png)
![$ [D]=\alpha([A]\bullet\{x\})\otimes(\{y\}\bullet[B])+[C] \quad\equiv\quad \TeFo{D}\gets\alpha(\TeFo{A}:\TeSe{x})\otimes(\TeSe{y}:\TeFo{B})+\TeFo{C} $](form_74.png)
![$ [B]=\alpha([B]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{B} $](form_75.png)
![$ [B]=\alpha([A]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{A} $](form_76.png)
![$ s=\{x\}^T[A]\{y\} \quad\equiv\quad s=\Dc{\Dc{\TeSe{x}}{\TeFo{A}}}{\TeSe{y}} $](form_77.png)
 1.4.7
1.4.7