| typedef blitz::TinyVector<REAL,6> Tensors::Tensor2 |
Second Order Tensor (Mandel representation) {{{.
Introducing a base of nine second order tensors, known as Mandel's basis (Brannon, 2000), second order tensors may be viewed as 9D vectors. If a tensor 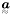 is symmetric, i.e.
is symmetric, i.e. 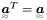 , then it may be represented by a 6D vector:
, then it may be represented by a 6D vector:
![\[ [\TeSe{a}] = \MaExpZ{a} \longrightarrow \begin{Bmatrix} a_{0}=a_{00} \\ a_{1}=a_{11} \\ a_{2}=a_{22} \\ a_{3}=\sqrt{2}a_{01} \\ a_{4}=\sqrt{2}a_{12} \\ a_{5}=\sqrt{2}a_{02} \end{Bmatrix} \]](form_40.png)
Therefore, Tensor2 is a vector with six (6) components, in which the last three components are equal to the Cartesian Components multiplied by 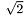 .
.
}}}
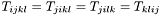 ) fourth order tensors can be represented as 6D second order tensors:
) fourth order tensors can be represented as 6D second order tensors:![\[ [\TeFo{T}] = \begin{bmatrix} T_{0000} & T_{0011} & T_{0022} & \sqrt{2}T_{0001} & \sqrt{2}T_{0012} & \sqrt{2}T_{0002} \\ T_{1100} & T_{1111} & T_{1122} & \sqrt{2}T_{1101} & \sqrt{2}T_{1112} & \sqrt{2}T_{1102} \\ T_{2200} & T_{2211} & T_{2222} & \sqrt{2}T_{2201} & \sqrt{2}T_{2212} & \sqrt{2}T_{2202} \\ \sqrt{2}T_{0100} & \sqrt{2}T_{0111} & \sqrt{2}T_{0122} & 2T_{0101} & 2T_{0112} & 2T_{0102} \\ \sqrt{2}T_{1200} & \sqrt{2}T_{1211} & \sqrt{2}T_{1222} & 2T_{1201} & 2T_{1212} & 2T_{1202} \\ \sqrt{2}T_{0200} & \sqrt{2}T_{0211} & \sqrt{2}T_{0222} & 2T_{0201} & 2T_{0212} & 2T_{0202} \\ \end{bmatrix} \]](form_46.png)
 1.4.7
1.4.7