Functions
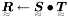 .
. 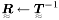 .
. 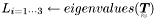 .
. 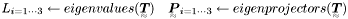 .
. 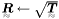 .
. Functions | |
| void | Tensors::Mult (Tensor2 const &S, Tensor2 const &T, Tensor2 &R) |
Tensor multiplication 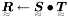 . . | |
| REAL | Tensors::Norm (Tensor2 const &T) |
| Euclidian norm of a symmetric 2nd order tensor. | |
| REAL | Tensors::Det (Tensor2 const &T) |
| Determinant of T. | |
| bool | Tensors::Inv (Tensor2 const &T, Tensor2 &R) |
Inverse of a tensor T 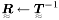 . . | |
| bool | Tensors::Eigenvals (Tensor2 const &T, REAL L[3]) |
Eigenvalues (L) of a tensor T 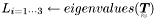 . . | |
| bool | Tensors::Eigenvp (Tensor2 const &T, REAL L[3], Tensor2 P[3]) |
Eigenvalues (L) and Eigenprojectors (P) of a tensor T 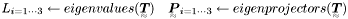 . . | |
| bool | Tensors::Sqrt (Tensor2 const &T, Tensor2 &R) |
Square root of a tensor T 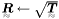 . . | |
| void | Tensors::CharInvs (Tensor2 const &T, REAL I[3]) |
| Characteristic invariants of a symmetric second order tensor. | |
| void | Tensors::Strain_Ev_Ed (Tensor2 const &Eps, REAL &Ev, REAL &Ed) |
| Strain Invariants. | |
| void | Tensors::Stress_p_q (Tensor2 const &Sig, REAL &p, REAL &q) |
| Stress Invariants (Cambridge). | |
| REAL | Tensors::Stress_q (Tensor2 const &Sig) |
| Cambridge's q deviatoric stress invariant. | |
| REAL | Tensors::Sin3ThDev (Tensor2 const &S) |
| Sin3Th given deviator (S) of the stress tensor. | |
| void | Tensors::Stress_p_q_S_sin3th (Tensor2 const &Sig, REAL &p, REAL &q, Tensor2 &S, REAL &sin3th) |
| Stress Invariants (Cambridge) + deviator of Sigma. | |
| bool | Tensors::Stress_tn_ts (Tensor2 const &Sig, REAL &tn, REAL &ts) |
| Stress Invariants (Professor Nakai's invariants). | |
| void | Tensors::Stress_P_Q (Tensor2 const &Sig, REAL &P, REAL &Q) |
| Stress Invariants (Professor Brannon's isomorphic invariants). | |
| void | Tensors::Stress_P_Q_S_sin3th (Tensor2 const &Sig, REAL &P, REAL &Q, Tensor2 &S, REAL &sin3th) |
| Stress Invariants (Professor Brannon's isomorphic invariants) + deviator of Sigma. | |
| REAL | Tensors::Sin3Th (REAL SI, REAL SII, REAL SIII) |
| Returns Sin3Th, given three principal values, which are not necessary sorted. | |
| void | Tensors::Hid2Sig (REAL const &p, REAL const &q, REAL const &th, REAL &Sig1, REAL &Sig2, REAL &Sig3) |
| Converts hidrostatic coordinates to sigma (principal) coord (T in radians). | |
| void | Tensors::Hid2Sig (REAL const *P, REAL const *Q, REAL const *T, REAL *SI, REAL *SII, REAL *SIII, int Size) |
| Converts hidrostatic coordinates to sigma (principal) coord (T in radians). | |
| void | Tensors::Hid2Sig_ (REAL const &SX, REAL const &SY, REAL const &p, REAL &SI, REAL &SII, REAL &SIII) |
| Converts hidrostatic coordinates (Sx, Sy, Sz) to sigma (principal) coord (T in radians). | |
Tensor multiplication 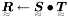 .
.
-*- IMPORTANT -*-
This function is valid only if the result R=S*T would be symmetric, however this is NOT always true, even if S and T are both symmetric !!!
| S | In: Left operand |
| T | In: Right operand |
| R | Out: R=S*T |
Definition at line 233 of file functions.h.
| REAL Tensors::Norm | ( | Tensor2 const & | T | ) | [inline] |
Euclidian norm of a symmetric 2nd order tensor.
| T | In: Tensor T |
Definition at line 257 of file functions.h.
Inverse of a tensor T 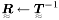 .
.
| T | In: Tensor T |
| R | Out: R=inv(T) |
Definition at line 269 of file functions.h.
| bool Tensors::Eigenvals | ( | Tensor2 const & | T, | |
| REAL | L[3] | |||
| ) | [inline] |
Eigenvalues (L) of a tensor T 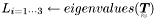 .
.
| T | In: Tensor T |
| L | Out: Eigenvalues of T |
Definition at line 288 of file functions.h.
Eigenvalues (L) and Eigenprojectors (P) of a tensor T 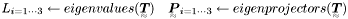 .
.
Any symmetric second order tensor 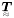 may be calculated according to its Spectral Decomposition:
may be calculated according to its Spectral Decomposition:
![\[ \TeSe{T} = L_0\TeFi{V}_0\otimes\TeFi{V}_0 + L_1\TeFi{V}_1\otimes\TeFi{V}_1 + L_2\TeFi{V}_2\otimes\TeFi{V}_2 \]](form_20.png)
in which 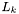 and
and 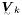 are the eigenvalues and eigenvectors of tensor
are the eigenvalues and eigenvectors of tensor 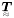 , respectively
, respectively
The eigenprojector is defined according to:
![\[ \TeSe{P}_k = \TeFi{V}_{(k)} \otimes \TeFi{V}_{(k)} \qquad no \quad sum \quad on \quad (k) \]](form_23.png)
Therefore, the spectral representation can be re-written as:
![\[ \TeSe{T} = L_0\TeSe{P}_0 + L_1\TeSe{P}_1 + L_2\TeSe{P}_2 \]](form_24.png)
Or, considering Einstein's summation rule (over index k, from 1 to 3)
![\[ \TeSe{T} = L_k \TeSe{P}_k \]](form_25.png)
The following properties hold for the eigenprojectors, in fact, for any projector (Brannon, 2000),
![\[ \TeSe{P}_i \bullet \TeSe{P}_j = \TeSe{P}_i \quad if \quad i = j \]](form_26.png)
![\[ \TeSe{P}_i \bullet \TeSe{P}_j = \TeSe{0} \quad if \quad i \ne j \]](form_27.png)
![\[ \TeSe{P}_1 + \TeSe{P}_2 + \TeSe{P}_3 = \TeSe{I} \]](form_28.png)
| T | In: Tensor T |
| L | Out: Eigenvalues of T |
| P | Out: Igenprojectors of T |
Definition at line 297 of file functions.h.
Square root of a tensor T 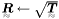 .
.
| T | In: Tensor T |
| R | Out: R=sqrt(T) |
Definition at line 335 of file functions.h.
| void Tensors::CharInvs | ( | Tensor2 const & | T, | |
| REAL | I[3] | |||
| ) | [inline] |
Characteristic invariants of a symmetric second order tensor.
| T | In: Tensor T |
| I | Out: Characterist invariants |
Definition at line 357 of file functions.h.
| void Tensors::Strain_Ev_Ed | ( | Tensor2 const & | Eps, | |
| REAL & | Ev, | |||
| REAL & | Ed | |||
| ) | [inline] |
Strain Invariants.
![\[ Eps=\TeSe{\varepsilon} \]](form_56.png)
![\[ Ev=\varepsilon_v=tr(\TeSe{\varepsilon}) \]](form_71.png)
![\[ Ed=\varepsilon_d=\sqrt{\nicefrac{2}{3}\TeSe{e}:\TeSe{e}} \quad \TeSe{e}=dev(\TeSe{\varepsilon})=\TeSe{\varepsilon}-\varepsilon_V\TeSe{I}/3 \]](form_72.png)
| Eps | In: Strain tensor Epsilon |
| Ev | Out: Volumetric strain |
| Ed | Out: Deviatoric strain |
Definition at line 365 of file functions.h.
| void Tensors::Stress_p_q | ( | Tensor2 const & | Sig, | |
| REAL & | p, | |||
| REAL & | q | |||
| ) | [inline] |
Stress Invariants (Cambridge).
![\[ Sig=\TeSe{\sigma} \]](form_59.png)
![\[ p=tr(\TeSe{\sigma})/3 \]](form_60.png)
![\[ q=\sqrt{\nicefrac{3}{2}\TeSe{S}:\TeSe{S}} \quad \TeSe{S}=dev(\TeSe{\sigma})=\TeSe{\sigma}-p\TeSe{I} \]](form_67.png)
| Sig | In: Stress tensor |
| p | Out: Cambridge mean stress |
| q | Out: Cambridge deviatoric stress |
Definition at line 374 of file functions.h.
| REAL Tensors::Stress_q | ( | Tensor2 const & | Sig | ) | [inline] |
Cambridge's q deviatoric stress invariant.
| Sig | In: Stress tensor |
Definition at line 383 of file functions.h.
| REAL Tensors::Sin3ThDev | ( | Tensor2 const & | S | ) | [inline] |
Sin3Th given deviator (S) of the stress tensor.
| S | Deviator of the stress tensor |
* * +30 S1 * 0-> | * -30 \ th| th: theta * ', \ | * '. \ | * '.\| * .' -. * .' '. * .' '. * S2 .' '. S3 * *
Definition at line 391 of file functions.h.
| void Tensors::Stress_p_q_S_sin3th | ( | Tensor2 const & | Sig, | |
| REAL & | p, | |||
| REAL & | q, | |||
| Tensor2 & | S, | |||
| REAL & | sin3th | |||
| ) | [inline] |
Stress Invariants (Cambridge) + deviator of Sigma.
| S | deviator of Sigma |
| sin3th | theta3 = theta*3 |
Definition at line 406 of file functions.h.
| bool Tensors::Stress_tn_ts | ( | Tensor2 const & | Sig, | |
| REAL & | tn, | |||
| REAL & | ts | |||
| ) | [inline] |
Stress Invariants (Professor Nakai's invariants).
![\[ Sig=\TeSe{\sigma} \]](form_59.png)
![\[ t_N=3\frac{I_3}{I2} \]](form_68.png)
![\[ t_S=\frac{\sqrt{I_1I_2I_3-9I_3^2}}{I_2} \]](form_69.png)
| Sig | In: Stress tensor |
| tn | Out: mean stress invariant |
| ts | Out: deviatoric stress invariant |
Definition at line 418 of file functions.h.
| void Tensors::Stress_P_Q | ( | Tensor2 const & | Sig, | |
| REAL & | P, | |||
| REAL & | Q | |||
| ) | [inline] |
Stress Invariants (Professor Brannon's isomorphic invariants).
![\[ Sig=\TeSe{\sigma} \]](form_59.png)
![\[ P=\sqrt{3}p \]](form_64.png)
![\[ Q=\sqrt{\TeSe{S}:\TeSe{S}} \quad \TeSe{S}=dev(\TeSe{\sigma})=\TeSe{\sigma}-p\TeSe{I} \]](form_95.png)
| Sig | In: Stress tensor |
| P | Out: Isomorphic mean stress |
| Q | Out: Isomorphic deviatoric stress |
Definition at line 438 of file functions.h.
| void Tensors::Stress_P_Q_S_sin3th | ( | Tensor2 const & | Sig, | |
| REAL & | P, | |||
| REAL & | Q, | |||
| Tensor2 & | S, | |||
| REAL & | sin3th | |||
| ) | [inline] |
Stress Invariants (Professor Brannon's isomorphic invariants) + deviator of Sigma.
| Sig | In: Stress tensor |
| P | Out: Isomorphic mean stress |
| Q | Out: Isomorphic deviatoric stress |
| S | deviator of Sigma |
Definition at line 447 of file functions.h.
 1.4.7
1.4.7