| |
 |

RW James Building, University of Cape Town
Rondebosch 7701, South Africa
[email protected]
+27 21 650 3366
NPO Registration Number: 037-269-NPO
|
|
| What is the Free High School Science Textbook? |
| The FHSST is the contribution of a group of young scientists towards furthering science education in South Africa. We aim to provide a free science textbook for Grades 10 - 12 to all South African learners. |
| Administration |
| Visit our project administration web pages hosted on Savannah. |
|
General editorial guidelines for authors contributing to the FHSST project
Download the
PDF Version of these Guidelines
- Chapters should begin with a brief introduction and motivation for the
chapter.
- With regards general editing:
- Units and indices: write $m.s^{-1}$ or $m/s$ not $\frac{m}{s}$, and use
maths mode (i.e. $km$ not km)
- Notation: Vectors should be capped with arrows (i.e.
$\overrightarrow{F}$), while $F$ denotes a magnitude only
- Use boldface to highlight directions of vectors
- All important definitions should be placed in a definition
box:
Latex
Source:
\begin{center}
\psshadowbox{
\begin{tabular}{c}
\textbf{Definition:}
{\em Displacement} is defined as the magnitude
and direction\\
of the
straight line joining one's starting point to one's
final\\
point.
\end{tabular}
}
\end{center}
Output:

- Put very important comments in a margin box:
Latex
Source:
\marginpar{
\psshadowbox{
\begin{tabular}{c}
Using
vectors is \\
an important \\
skill you
\textbf{MUST}\\
master!
\end{tabular}
}
}
Output:

- Put text boxes around important equations together with key:
Latex
Source:
\begin{center}
\psshadowbox{
\begin{tabular}{rl}
\multicolumn{2}{c}{$\overrightarrow{p}
= m\overrightarrow{v}$}\\
\\
$\overrightarrow{p}$&: momentum
($kg.m.s^{-1}$ + direction)\\
$m$&: mass
($kg$)\\
$\overrightarrow{v}$&: velocity ($m.s^{-1}$ +
direction)\\
\end{tabular}
}
\end{center}
Output:
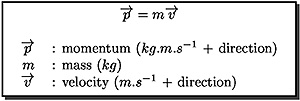
- Typical exam-type questions should be included as worked examples. Worked
examples should be added using the physics worked example environment `pwex'.
A title must be specified for the worked example and answers should be broken
down into logical steps each beginning with the `step' command. Keep the
explanations of each step concise without loss of clarity (we don't want to
scare learners off with lengthy solutions-- it looks
intimidating):
Latex Source:
\begin{pwex}{Subtracting
vectors algebraically I}
\textbf{Question:} Suppose that a tennis ball is
thrown horizontally
towards a wall at $3m.s^{-1}$ to the right. After
striking the wall,
the ball returns to the thrower at $2m.s^{-1}$.
Determine the change
in velocity of the
ball.
\textbf{Answer:}
\step
Remember that velocity is a vector.
The change in the velocity of the
ball is equal to the difference between
the ball's initial and
final
velocities:
\begin{eqnarray*}
\Delta\overrightarrow{v} & =
& \overrightarrow{v}_{final}
-
\overrightarrow{v}_{initial}
\end{eqnarray*}
Since the ball
moves along a straight line (i.e. left and right), we
can use the algebraic
technique of vector subtraction just discussed.
\step
Let's make to
the right the \textbf{positive}
direction. This means that to the left
becomes the \textbf{negative}
direction.
\step
With right
positive:
\begin{eqnarray*}
\overrightarrow{v}_{initial} & = &
+3m.s^{-1} \\
& and & \\
\overrightarrow{v}_{final} & =
& -2m.s^{-1}
\end{eqnarray*}
\step
Thus, the change in
velocity of the ball is:
\begin{eqnarray*}
\Delta\overrightarrow{v}
& = & (-2m.s^{-1}) - (+3m.s^{-1}) \\
& = &
(-5)m.s^{-1}
\end{eqnarray*}
Remember that in this case \underline{right
means positive} so:
\begin{eqnarray*}
\Delta\overrightarrow{v} & =
& 5m.s^{-1} \rm{\bf \ to \ the \
\emph{left}}
\end{eqnarray*}
\end{pwex}
Output:

- Remember to include interesting facts in your chapters. Use a
`psshadowbox' for this:
Latex
Source:
\vspace{3mm}
\psshadowbox{
\begin{tabular}{l}
\textbf{Interesting
fact}: The word `electron' comes from the Greek
word for \\
amber! The
ancient Greeks observed that if you rubbed a
piece of amber,\\
you
could use it to pick up bits of straw. (Attractive
electrostatic force!)\\
\end{tabular}
}
\vspace{3mm}
Output:

- Each chapter should have a conclusion.
- Each chapter should end with a summary of the important definitions,
quantities and equations introduced in the chapter:
Latex
Source:
\section{Summary of Important Quantities, Equations and
Concepts}
\begin{table}[b]
\begin{center}
\begin{tabular}{|c|c|ccc|c|}\hline
\hline
Quantity & Symbol &
\multicolumn{3}{c|}{S.I.
Units}
& Direction\\ \hline
Momentum & $\overrightarrow{p}$
& \multicolumn{3}{c|}{$kg.m.s^{-1}$}
& \checkmark\\ \hline
Mass
& $m$ & \multicolumn{3}{c|}{$kg$} & --- \\\hline
Velocity &
$\overrightarrow{u}$,$\overrightarrow{v}$
&
\multicolumn{3}{c|}{$m.s^{-1}$} & \checkmark \\ \hline
Change
in momentum & $\Delta \overrightarrow{p}$
&
\multicolumn{3}{c|}{$kg.m.s^{-1}$} & \checkmark\\ \hline
Force & $\overrightarrow{F}$ & $kg.m.s^{-2}$ & \textbf{or}
& $N$ & \checkmark \\\hline
Impulse & --- & $kg.m.s^{-1}$
& \textbf{or} & $N.s$ & \checkmark\\
\hline\hline
\end{tabular}
\end{center}
\caption{Summary of the
symbols and units of the quantities used in \textbf{Momentum} }
\label{table:momemtum::units}
\end{table}
\begin{description}
\item[Momentum]
The {\em momentum} of an object is defined as its
mass multiplied by its
velocity.
\item[Momentum of a System] The {\em total momentum of a
system}
is the sum of the momenta of each of the objects in the
system.
\item[Principle of Conservation of Linear Momentum:] `The total
linear
momentum of an isolated system is constant' or `In an
isolated
system the total momentum before a collision (or explosion) is
equal
to the total momentum after the collision (or
explosion)'.
\item[Law of Momentum:] The applied resultant force acting on
an
object is equal to the rate of change of the object's momentum
and
this force is in the direction of the change in
momentum.
\end{description}
Output:

|
|